

5.5: Functions with Several Independent Variables The discussion has focussed on systems having only a single function y(x) such that the functional is an extremum.The following example of a cylindrically-symmetric soap-bubble surface formed by blowing a soap bubble that stretches between two circular hoops, illustrates the importance of the independent variable. Selecting which variable to use as the independent variable does not change the physics of a problem, but some selections can simplify the mathematics for obtaining an analytic solution. 5.4: Selection of the Independent Variable A wide selection of variables can be chosen as the independent variable for variational calculus.The Brachistochrone problem stimulated the development of the calculus of variations by John Bernoulli and Euler. 5.3: Applications of Euler’s Equation The Brachistochrone problem involves finding the path having the minimum transit time between two points.

Variational calculus, developed for classical mechanics, now has become an essential approach to many other disciplines in science, engineering, economics, and medicine.
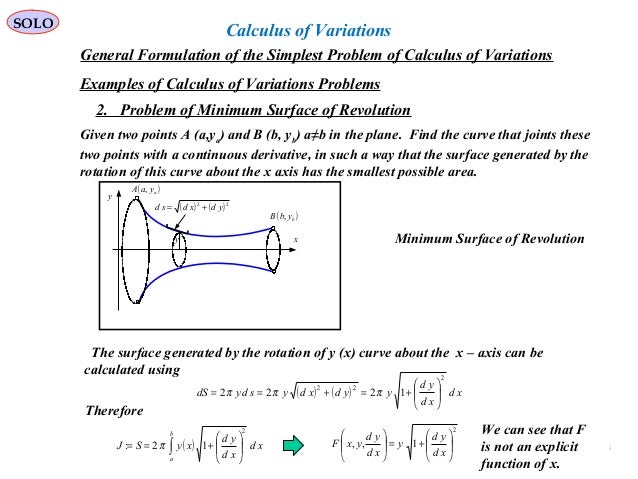
5.2: Euler’s Differential Equation The calculus of variations, presented here, underlies the powerful variational approaches that were developed for classical mechanics.He solved the brachistochrone problem which involves finding the path for which the transit time between two points is the shortest. 5.1: Introduction to the Calculus of Variations During the 18th century, Bernoulli, who was a student of Leibniz, developed the field of variational calculus which underlies the integral variational approach to mechanics.


 0 kommentar(er)
0 kommentar(er)
